If you are new to programming, you've probably been given a task to write a factorial number algorithm. Of course, you can do it iteratively, like this:
#include <stdio.h>
int iterative_factorial(int number)
{
int result;
result = number;
if (number <= 0)
{
if (number == 0)
return (1);
else
return (number);
}
while (number > 1)
{
result *= (number - 1);
number--;
}
return (result);
}
int main()
{
int number;
number = iterative_factorial(4);
printf("The result is: %d\n", number);
}
Output:
The result is: 24
I will not get into the details of this, but we can put this line printf("The number is %d and the result is %d\n", number, result) inside the loop to have a better visualization:
The number is 4 and the result is 4
The number is 3 and the result is 12
The number is 2 and the result is 24
The result is: 24
There's not a problem with this code and we saved a few lines by iterating the number itself, and not using a iterator i. But our code can look a lot cleaner if we use recursion.
A recursive function is defined as a function that calls itself during the execution of the program. In this example, we will receive a number and call the function with number - 1 until number equals to 1:
int recursive_factorial(int number)
{
int result;
if (number <= 0)
{
if (number == 0)
return (1);
else
return (number);
}
result = 1;
if (number > 1)
{
result = (number * recursive_factorial(number - 1));
}
return (result);
}
int main()
{
int number;
number = recursive_factorial(4);
printf("The result is: %d\n", number);
}
During the first call, number = 4. The condition to call the function number > 1 is met and result = 4 * (recursive_factorial(3)).
On the second call, number = 3 and result = 3 * (recursive_factorial(2)).
On the third call, number = 2 and result = 2 * (recursive_factorial(1)).
Finally, on the fourth call, number = 1 and we cannot call the function again, since the number must be > 1. So, we return result which is equal to 1.
A recursive function works in a way that when we finally get a return (meaning when we don't have to call the function again), it starts to trace back to the previous calls.
When the function goes back to the third call, it now knows that recursive_factorial(1) = 1. So, result = 2 * 1 = 2 and the third call returns 2. So, we can conclude that recursive_factorial(2) = 2.
Let's go back to the second call. Since recursive_factorial(2) = 2, we can calculate the return result = 3 * 2 = 6. So, recursive_factorial(3) = 6.
Now, the first call needed the result of recursive_factorial(3), which is 6. Since We can now calculate the final result, which is result = 4 * 6 = 24. The final result is 24 (4 * 3 * 2 * 1).
Here's a image that might help visualize all of the process:
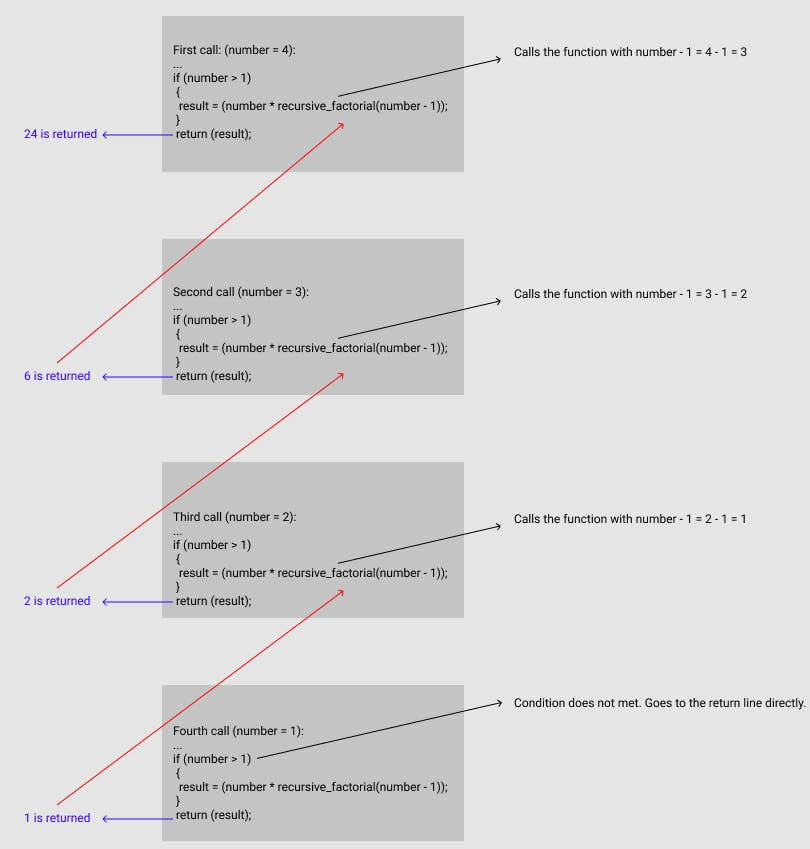
Also, if we put this line of code printf("Result is %d\n", result) right before the
return (result) line, the output is:
Result is 1
Result is 2
Result is 6
Result is 24
The result is: 24
Here it goes! I hope you learned a little bit about recursion. It's not the best when you want performance (since you run your function n number of times), but understanding this concept is very important because recursion is used in data structures.
Want to challenge yourself? Try coding a recursive Fibonacci algorithm!
